Skip to main content

斐波那切数列

递归​

最简单、容易理解的写法，缺点是调用栈大，复杂度高

const fibonacci = function(n) {
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    return fib(n - 1) + fib(n - 2);
};

优化方向：查表，复用计算结果，避免重复计算

尾递归​

/**
 * @param {number} n
 * @return {number}
 */
const fib = function (n, result1 = 0, result2 = 1) {
    if (n === 0) {
        return result1;
    }
    return fib(n - 1, result2, result1 + result2);
};

迭代​

const fib = function (n) {
    if (n === 0 || n === 1) {
        return n;
    }
    let prev = 0,
        cur = 1;

    for (let i = 1; i < n; i++) {
        [cur, prev] = [cur + prev, cur];
    }
    return cur;
};

矩阵快速幂解法​

原理：​

如果a为矩阵，等式同样成立，后面我们会用到它。
假设有矩阵2*2矩阵A，满足下面的等式：
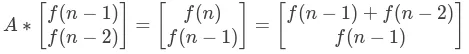
image.png

可以得到矩阵A：
image.png

因此也就可以得到下面的矩阵等式：
image.png

再进行变换如下：
image.png

以此类推，得到：
image.png

实际上f(n)就是矩A^(n-1)中的A[0][0],或者是矩A^n中的A[0][1]。

那么现在的问题就归结为，如何求A^n，其中A为2*2的矩阵。根据我们最开始的公式，很容易就有思路，代码实现如下：

const matrix = [
    [1, 1],
    [1, 0],
];

const matrixPow = n => {
    let result = [
        [1, 1],
        [1, 0],
    ];
    for (let i = 1; i < n; i++) {
        let newResult = [[], []];
        newResult[0][0] =
            matrix[0][0] * result[0][0] + matrix[0][1] * result[1][0];
        newResult[0][1] =
            matrix[0][0] * result[0][1] + matrix[0][1] * result[1][1];
        newResult[1][0] =
            matrix[1][0] * result[0][0] + matrix[1][1] * result[1][0];
        newResult[1][1] =
            matrix[1][0] * result[0][1] + matrix[1][1] * result[1][1];
        result = newResult;
    }

    return result;
};

const fib = n => {
    if (n === 0) {
        return 0;
    }

    const fibMatrix = matrixPow(n - 1);
    return fibMatrix[0][0];
};