Skip to main content

快慢指针

141. Linked List Cycle​

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function (head) {
    var p = head,
        q = head;
    while (q != null && q.next != null && q.next.next != null) {
        p = p.next;
        q = q.next.next;
        if (p == q) {
            return true;
        }
    }

    return false;
};

142.Linked List Cycle II​

这道题的解决方案如下：

  1. 首先快慢指针，找到相遇点，确认有环；
  2. 此时一个指针继续从相遇点前进，一个新的指针，从 head 出发。
  3. 两者相遇点，为第一个入环节点。

证明如下： 

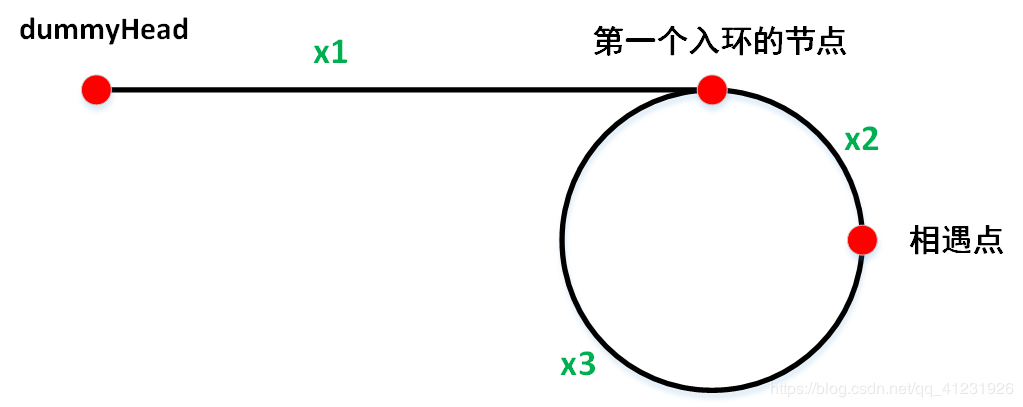
 快慢指针在相遇点相遇时，二者走过的距离分别为：  
 x1 + x2 + k1 * (x2 + x3)  
 x1 + x2 + k2 * (x2 + x3)  
 由二者速度可知，  
 2 * ( x1 + x2 + k1 * (x2 + x3)) = x1 + x2 + k2 * (x2 + x3);  
 x1 + x2 + 2 * k1 * (x2 + x3) =  k2 * (x2 + x3);  
 x1 - x3 + 2 * k1 * (x2 + x3) =  (k2 - 1 ) * (x2 + x3);  
 x1 - x3 =  (k2 - 2 * k1 - 1 ) * (x2 + x3);

由此可知，x1 - x3，也就是第二次遍历是两个指针走过的距离差，正好是 x2 + x3 ，也就是环的长度的整数倍。由此，两个指针必然在第一个入环的节点相遇。

20190108231208711.png

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const detectCycle = function (head, pos) {
    let p = head,
        q = head;
    while (q && q.next && q.next.next) {
        p = p.next;
        q = q.next.next;
        if (p == q) {
            while (head != p) {
                p = p.next;
                head = head.next;
            }
            return p;
        }
    }

    return null;
};