Dijkstra

大名鼎鼎的最短路径算法，不再赘述

数据结构

// 输入，每个节点的next节点，距离；以及是否遍历过改节点
const graph = {
  A: {
    neighbours: {
      B: 22,
      ...
    },
    done: false;
  },
  B: {...},
  ...
}


// 每个节点的最小cost
const = {
  A: 0,
  B: 22,
  ...
}

// 最小cost对应的前一节点
parent = {
  A: 'B'
}

算法步骤

• 找出距离最短的节点
  • 遍历其 neighbours
  • 如果计算出 neighbour 的 cost 小于其当前 cost，更新 neighbour 的 cost
  • 对该节点标记完成
• 重复上述步骤。

示例

如下图所示，寻找从 起点 A 到 终点 F 的最短路径。

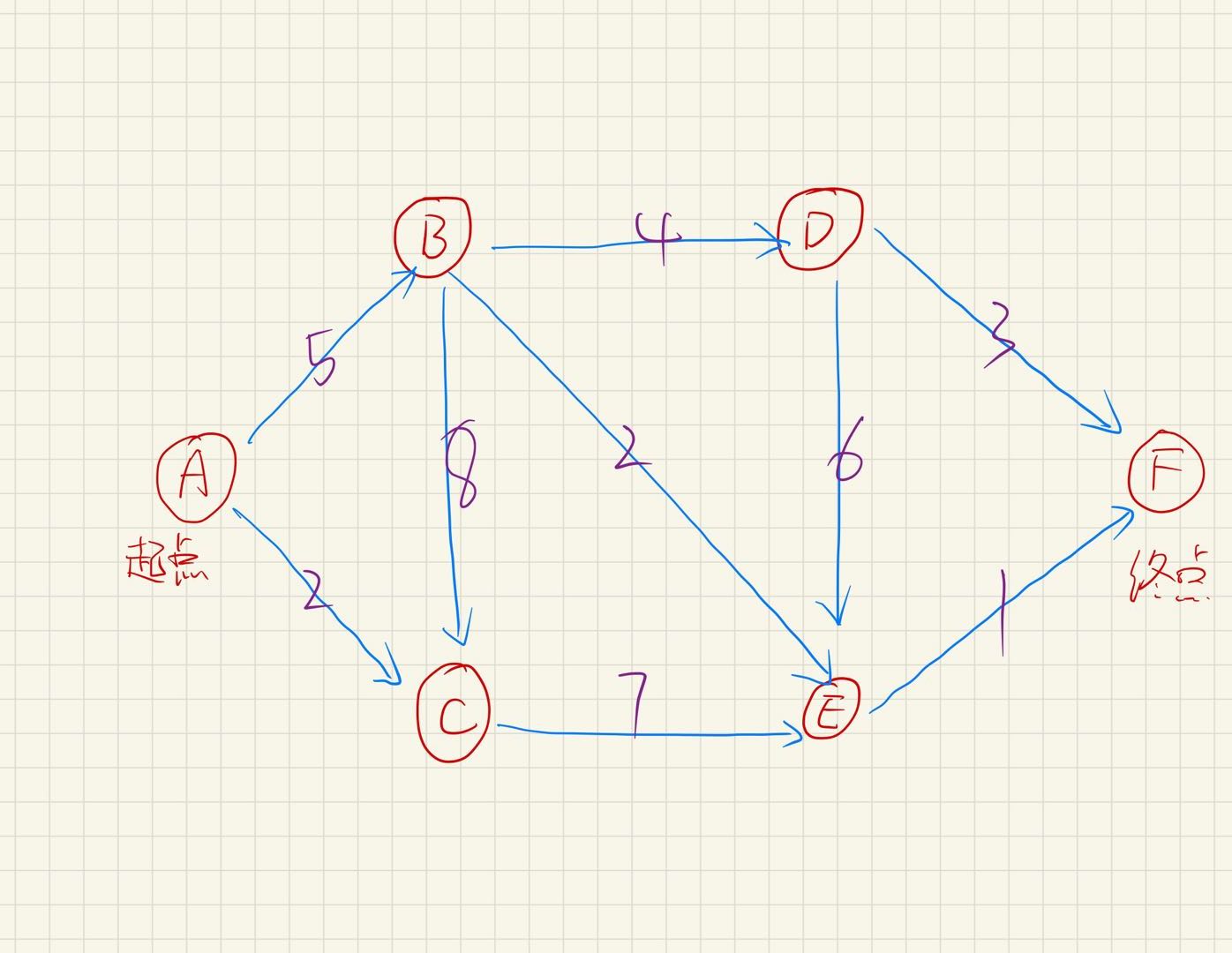
// graph, 用以描述问题
const graph = {
    A: { neighbours: { B: 5, C: 2 }, done: false },
    B: { neighbours: { D: 4, E: 2 }, done: false },
    C: { neighbours: { B: 8, E: 7 }, done: false },
    D: { neighbours: { E: 6, F: 3 }, done: false },
    E: { neighbours: { F: 1 }, done: false },
    F: { neighbours: {}, done: false }
};

// 获取未处理的，最近的点
const getNearestNode = (costs, graph) => {
    const sortedKeys = Object.keys(costs)
        .filter(key => !graph[key].done)
        .sort((a, b) => costs[a] - costs[b]);
    return sortedKeys[0];
};

function dijkstra(graph) {
    // 先记录起始点，为0
    const costs = {
        A: 0
    };

    const parents = {};
    let key;
    while ((key = getNearestNode(costs, graph))) {
        const nbs = graph[key].neighbours;
        for (const nb of Object.keys(nbs)) {
            const cost = costs[key];
            if (!costs[nb] || costs[nb] > cost + nbs[nb]) {
                costs[nb] = cost + nbs[nb];
                parents[nb] = key;
            }
        }
        graph[key].done = true;
    }
    console.log(costs);
    console.log(parents);
}

dijkstra(graph);

// 结果如下
// costs
{ A: 0, B: 5, C: 2, E: 7, D: 9, F: 8 }
// parents
{ B: 'A', C: 'A', E: 'B', D: 'B', F: 'E' }

应用

Leetcode 743. Network Delay Time
代码如下

/**
 * @param {number[][]} times
 * @param {number} N
 * @param {number} K
 * @return {number}
 */
const generateGraph = times => {
    const graph = {};
    for (const [t0, t1, t2] of times) {
        if (!graph[t0]) {
            graph[t0] = { neighbours: {} };
        }
        if (!graph[t1]) {
            graph[t1] = { neighbours: {} };
        }
        graph[t0].neighbours[t1] = t2;
    }
    return graph;
};

const getNearestNode = (costs, graph) => {
    const sortedKeys = Object.keys(costs)
        .filter(key => !graph[key].done)
        .sort((a, b) => costs[a] - costs[b]);
    return sortedKeys[0];
};

var networkDelayTime = function (times, N, K) {
    const graph = generateGraph(times);
    const costs = { [K]: 0 };
    const parents = {};

    let key;
    while ((key = getNearestNode(costs, graph))) {
        const nbs = graph[key].neighbours;
        for (const nb of Object.keys(nbs)) {
            const cost = costs[key];
            if (costs[nb] === undefined || costs[nb] > cost + nbs[nb]) {
                costs[nb] = cost + nbs[nb];
                parents[nb] = key;
            }
        }
        graph[key].done = true;
    }

    if (Object.keys(costs).length !== N) {
        return -1;
    }
    return Math.max(...Object.values(costs));
};

console.log(
    networkDelayTime(
        [
            [2, 1, 1],
            [2, 3, 1],
            [3, 4, 1],
        ],
        4,
        2,
    ),
);
console.log(
    networkDelayTime(
        [
            [1, 2, 1],
            [2, 1, 3],
        ],
        2,
        2,
    ),
);